A Newsvendor Formulation of the Army and Army Reserve
Walter Bennette
05-01-2014
Overview
- Problem Statement
- Background and Justification
- Model
- Analysis
- Worth of Project
Problem Statement

The Army Reserve can be thought of as a strategic reserve for the Army.
Problem Statement
- Soldiers voluntarily join the Army Reserve
- Work/train 38 days per year
- Receive some benefits
- Work a regular job
- Could be called into full time service
A relatively inexpensive inventory of soldiers ready for action
Problem Statement
Question: How many troops should be in the Army Reserve?
Answer:
Problem Statement
Question: How many troops should be in the Army Reserve?
Answer: Develop an inventory model to aide in this decision.
Background and Justification
Army Reserve:
- Began in 1908
- 205,000 strong (compare to 541,000 in the Army)
- Can be called to active duty
- Work 38 days a year
- $3,216 per year
Background and Justification
Whats the right size for the US army?
- Current budget proposal calls for reduction
- Defense analyst thinks the size should increase
Background and Justification
- We can use an inventory model to find the economically optimal decision.
- This is crucial for fiscal responsibility
Model
Newsvendor:
- Products lose value after time
- Only one opportunity to place an order
- Distribution of demand
- Holding cost
- Shortage cost
Model
Newsvendor meets Army Reserve
Products lose value after time:
- Soldiers have a limited shelf life. (Assume 8 years)
- How many old soldiers do you know?
Model
Newsvendor meets Army Reserve
Products lose value after time:
- Soldiers have a limited shelf life. (Assume 8 years)
How many old soldiers do you know?

Model
Newsvendor meets Army Reserve
Only one opportunity to place an order:
- Assume they place an order every 8 years
- This is a simplifying assumption
- How many would sign up during war?
Model
Newsvendor meets Army Reserve
Only one opportunity to place an order:
- Assume they place an order every 8 years
- This is a simplifying assumption
- How many would sign up during war?

Model
Newsvendor meets Army Reserve
Distribution of demand:
- Historical data
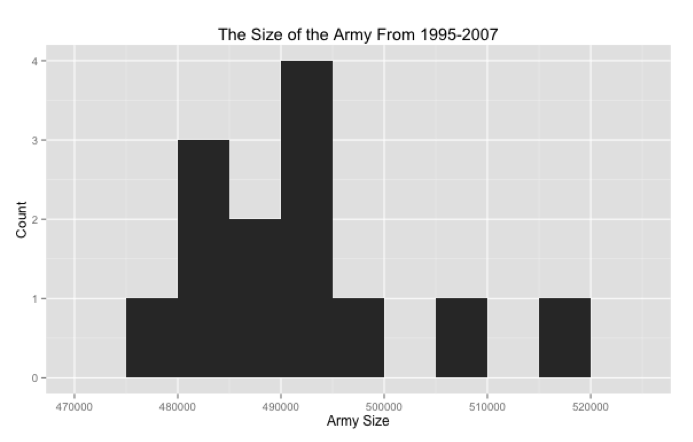
Model
Newsvendor meets Army Reserve
Holding cost:
- Cost to recruit ($15,000)
- Cost to pay ($3,216 a year)
Model
Newsvendor meets Army Reserve
Shortage cost:
- Unknown
- Loss of life and loss of freedoms
- Can make a guess through analysis
Analysis
Calucluate Shortage Cost
- Known demand distribution
- Assume current troop level (S) is optimal
- \( S^*=F^{-1}\left(\frac p{h+p} \right) \)
- \( p=\frac{hF(S)}{1-F(S)} \)
Analysis
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( S=746,291 \)
\( h=40,728 \ dollars \)
\( p=\frac{hF(S)}{1-F(S)}=Infinity \)
\( Type \ I \ service \ level=100\% \)
\( Type \ II \ service \ level=100\% \)
Analysis
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( S=746,291 \)
\( h=40,728 \ dollars \)
\( p=\frac{hF(S)}{1-F(S)}=Infinity \)
\( Type \ I \ service \ level=100\% \)
\( Type \ II \ service \ level=100\% \)
Obviously troop levels are not determined with an economic model (or we have the wrong model)
Analysis
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( S=643,791 \)
\( h=81,456 \ dollars \)
\( p=\frac{hF(S)}{1-F(S)}=7.4 \ trillion \ dollars \)
\( Type \ I \ service \ level \approx 100\% \)
\( Type \ II \ service \ level \approx 100\% \)
Analysis
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( S=643,791 \)
\( h=81,456 \ dollars \)
\( p=\frac{hF(S)}{1-F(S)}=7.4 \ trillion \ dollars \)
\( Type \ I \ service \ level \approx 100\% \)
\( Type \ II \ service \ level \approx 100\% \)
Refinements must be made to the model
Analysis
Allow the decision to be made on service level
Type I:
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( \alpha=0.999 \)
\( h=81,456 \ dollars \)
\( S^{\alpha}=F^{-1}\left(\frac {\frac{h\alpha}{(1-\alpha)}}{h+\left(\frac{h\alpha}{(1-\alpha)} \right)} \right) = 594,239 \)
\( Reserve=52,948 \)
Analysis
Allow the decision to be made on service level
Type I:
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( \alpha=0.999 \)
\( h=81,456 \ dollars \)
\( S^{\alpha}=F^{-1}\left(\frac {\frac{h\alpha}{(1-\alpha)}}{h+\left(\frac{h\alpha}{(1-\alpha)} \right)} \right) = 594,239 \)
\( Reserve=52,948 \)
Demand met for 99.9% of planning periods
Analysis
Allow the decision to be made on service level
Type II:
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( \beta=0.999 \)
\( h=81,456 \ dollars \)
\( S^{\beta}=\sigma L^{-1}\left(\frac{\mu \left(1-\beta \right)}{\sigma} \right)+\mu=566,820 \)
\( Reserve=25,529 \)
Analysis
Allow the decision to be made on service level
Type II:
\( \mu=541,291 \)
\( \sigma=17,134 \)
\( \beta=0.999 \)
\( h=81,456 \ dollars \)
\( S^{\beta}=\sigma L^{-1}\left(\frac{\mu \left(1-\beta \right)}{\sigma} \right)+\mu=566,820 \)
\( Reserve=25,529 \)
99.9% of demand met
Project Worth
- Prelim results indicate the Army may be too large
- Obviously the inventory model needs to be refined
- Similar techniques could be used to aide decision making
Questions?

Questions?
Walter Bennette
bennette@iastate.edu
bennette.github.io