Solving a problem through mathematical modeling
Walter Bennette
12 - 06 - 2013
Steps to follow
- Identify the problem to be solved
- Define what constitutes a solution
- Find constraints on valid solutions
- Decide what type of solution is optimal
- Construct a model
- Solve
Peculiar Car Rental
- Owned and operated by Joe
- Joe has started having to turn customers away
Joe hopes he can earn more money by identifying the correct customers to turn away

Peculiar Car Rental has some peculiar rental practices
- Reservations are placed Sunday for the week ahead
- Reservations are confirmed Sunday evening
- No cars are rented on Sunday
- There are \( m \) cars to rent each day
- All cars are identical
Identify the problem to be solved
What needs to be done?
- Choose which reservations to honor
- Do so in a way that maximizes profit
Define what constitutes a solution
- Need to assign cars to customers
- Car \( i = 1, ... , m \)
- Customer \( j = 1, ... , n \)
- Decision variable
- \( x_{ij} \in \{0, 1\} \)
- If \( x_{ij} = 1 \), customer \( j \) gets car \( i \)
- If \( x_{ij} = 0 \), customer \( j \) did not get car \( i \)
- \( x_{ij} \in \{0, 1\} \)
Find constraints on valid solutions
- A customer \( j \), should get no more than one car \( i \)
- \( \sum\limits_{i = 1}^{m} x_{ij} \leq 1 \space\space \space \space j = 1, ... , n \)
- For three cars and two customers
- Customer 1: \( \space x_{1, 1} + x_{2, 1} + x_{3, 1} \leq 1 \)
- Customer 2: \( \space x_{1, 2} + x_{2, 2} + x_{3, 2} \leq 1 \)
Find constraints on valid solutions
- A car \( i \), should be assigned to no more than one customer \( j \), at a time
- Need a concept of time
- Can break time into \( H \space \) time slots
- Then define \( J_t \) to be the set of customers, \( j \), that need a car, \( i \), at time \( t \).
- \( p_j = Days \space customer \space j \space needs \space a \space car \)
- \( p_1 = \{ M, T \} \)
- \( p_2 = \{ M \} \)
- \( J_M = \{Customer 1, Customer 2 \} \)
- \( J_T = \{Customer 1 \} \)
Find constraints on valid solutions
- A car \( i \), should be assigned to no more than one customer \( j \), at a time, \( J_t \)
- \( \sum\limits_{j\space \in \space J_t} x_{ij} \leq 1 \space\space \space i = 1, ... , m, \space\space \space t = 1, ..., H \)
- For two cars and two customers:
\( J_M = \{Customer 1, Customer 2 \} \)
\( J_T = \{Customer 1 \} \)- Car 1, Monday: \( \space x_{1, 1} + x_{1, 2} \leq 1 \)
- Car 2, Monday: \( \space x_{2, 1} + x_{2, 2} \leq 1 \)
- Car 1, Tuesday: \( \space x_{1, 1} \leq 1 \)
- Car 2, Tuesday: \( \space x_{2, 1} \leq 1 \)
- Car 1, Monday: \( \space x_{1, 1} + x_{1, 2} \leq 1 \)
- For two cars and two customers:
Decide what type of solution is optimal
- The answer should maximize the profit of Peculiar Car Rental
- Car \( i \) costs \( \pi_i \) to rent per day
- Customer \( j \), needs the car for \( |p_j| \) days
- \( w_{ij} = |p_j| \space \pi_i \)
- \( max \sum\limits_{i = 1}^{m} \sum\limits_{j = 1}^{n} \space w_{ij} x_{ij} \)
- For two cars that cost $10 per day
- For two customers that each want the car for 3 days
- \( max \space 30x_{1,1} + 30x_{1,2} + 30x_{2,1} + 30x_{2,2} \)
Construct a model
- We have decision variables
- We have constraints
- We have an objective function
\( max \sum\limits_{i = 1}^{m} \sum\limits_{j = 1}^{n} \space w_{ij} x_{ij} \)
\( s.t \)\( \sum\limits_{i\space= \space 1}^{m} x_{ij} \leq 1 \space\space \space \space j = 1, ... , n \)
\( \sum\limits_{j\space \in \space J_t} x_{ij} \leq 1 \space\space \space i = 1, ... , m, \space\space \space t = 1, ..., H \)
\( x_{ij} \in \{0, 1\} \)
Solve
This is an integer program, it can be solved through branch and bound!
Example
Lets give it a go!

Example: Data
Joe has three cars
i CAR COST 1 CAR1 $10 2 CAR2 $10 3 CAR3 $10 Six customers are interested in renting a car.
j CUSTOMER M T W R F S 1 ABBY 1 1 0 0 0 0 2 AL 0 0 1 1 1 1 3 BARB 1 1 1 1 1 0 4 BRUCE 0 1 1 1 0 0 5 CARL 1 1 1 0 0 0 6 CINDY 0 0 0 1 1 1
Example: LINGO Model
We need to rethink this constraint because I am not the best Lingo Modeler…
\( \sum\limits_{j\space \in \space J_t} x_{ij} \leq 1 \space\space \space i = 1, ... , m, \space\space \space t = 1, ..., H \)
Example: LINGO Model
| j | CUSTOMER | M |
|---|---|---|
| 3 | BARB | 1 |
| 4 | BRUCE | 0 |
- As described
- Car 1, Monday: \( \space x_{1, 3} \leq 1 \)
- Car 2, Monday: \( \space x_{2, 3} \leq 1 \)
- Car 3, Monday: \( \space x_{3, 3} \leq 1 \)
- Equivalent formulation
- Car 1, Monday: \( \space 1x_{1, 3} + 0x_{1,4} \leq 1 \)
- Car 2, Monday: \( \space 1x_{2, 3} + 0x_{2,4} \leq 1 \)
- Car 3, Monday: \( \space 1x_{3, 3} + 0x_{3,4} \leq 1 \)
Example: LINGO Model
LINGO:
SETS:
CAR: COST;
CUSTOMER: M, T, W, R, F, S;
DV (CAR, CUSTOMER): X;
ENDSETSExample: LINGO Model
LINGO:
DATA: CAR COST= CAR1 10 CAR2 10 CAR3 10; CUSTOMER M T W R F S= ABBY 1 1 0 0 0 0 AL 0 0 1 1 1 1 BARB 1 1 1 1 1 0 BRUCE 0 1 1 1 0 0 CARL 1 1 1 0 0 0 CINDY 0 0 0 1 1 1; ENDDATA
Example: LINGO Model
Model:
\( max \sum\limits_{i = 1}^{m} \sum\limits_{j = 1}^{n} \space w_{ij} x_{ij} \)
LINGO:
MAX = @SUM(CAR( I):
@SUM(CUSTOMER( J):
!Days customer J needs a car;
(M( J) + T( J) + W( J) + R( J) + F( J) + S( J))*
!Cost of renting car I per day;
COST( I) *
!Decision to rent car J to cutomer I;
X( I, J)));
Example: LINGO Model
Model:
\( \sum\limits_{i\space= \space 1}^{m} x_{ij} \leq 1 \space\space \space \space j = 1, ... , n \)
LINGO:
!Constraint for each customer; @FOR(CUSTOMER( J): !Each customer gets at most one car; @SUM(CAR( I): X( I,J)) <= 1);
Example: LINGO Model
Model:
\( \sum\limits_{j\space \in \space J_t} x_{ij} \leq 1 \space\space \space i = 1, ... , m, \space\space \space t = 1, ..., H \)
LINGO:
!Constraint for each car; @FOR(CAR( I): !Each car has at most one customer on Monday; @SUM(CUSTOMER( J): M( J)*X( I, J)) <= 1);
!Constraint for each car; @FOR(CAR( I): !Each car has at most one customer on Tuesday; @SUM(CUSTOMER( J): T( J)*X( I, J)) <= 1);
...
Example: LINGO Model
Model:
\( x_{ij} \in \{0, 1\} \)
LINGO:
!Each Car; @FOR(CAR( I): !Each Customer @FOR(CUSTOMER( J): !The decision variables need to be binary; @BIN(X( I,J))));
Example: Solution
| CUST | M | T | W | R | F | S |
|---|---|---|---|---|---|---|
| ABBY | 1 | 1 | 0 | 0 | 0 | 0 |
| AL | 0 | 0 | 1 | 1 | 1 | 1 |
| BARB | 1 | 1 | 1 | 1 | 1 | 0 |
| BRUCE | 0 | 1 | 1 | 1 | 0 | 0 |
| CARL | 1 | 1 | 1 | 0 | 0 | 0 |
| CINDY | 0 | 0 | 0 | 1 | 1 | 1 |
| DV | Value |
|---|---|
| X( CAR1, BARB) | 1 |
| X( CAR2, ABBY) | 1 |
| X( CAR2, AL) | 1 |
| X( CAR3, CARL) | 1 |
| X( CAR3, CINDY) | 1 |
Example: Solution
Objective value: 170
Solution: reject Bruce's reservation, accept all others
Example: Solution procedure
Need to augment the data to show the solution procedure.
DATA: CAR COST= CAR1 10 CAR2 10 CAR3 10 CAR4 10 CAR5 10 CAR6 10 CAR7 10 CAR8 10 CAR9 10 CAR10 10 CAR11 10 CAR12 10 CAR13 10 CAR14 10 CAR15 10;
Example: Solution procedure
CUSTOMER M T W R F S= ABBY 1 1 0 0 0 0 AL 0 0 1 1 1 1 BARB 1 1 1 1 1 0 BRUCE 0 1 1 1 0 0 CARL 1 1 1 0 0 0 CINDY 0 0 0 1 1 1 DAN 1 1 0 0 0 0 DEB 1 0 1 0 0 0 FRAN 1 0 0 1 0 0 FRANK 1 0 0 0 1 0 JILL 1 0 0 0 0 1 JIM 0 1 1 0 0 0 LEON 0 1 0 1 0 0 LINDA 0 1 0 0 1 0 MARK 0 1 0 0 0 1 MARY 0 0 1 1 0 0 NICK 0 0 1 0 1 0 NINA 0 0 1 0 0 1 PAM 0 0 0 1 1 0 PETE 0 0 0 1 0 1 RANDY 0 0 0 0 1 1 RITA 1 1 1 0 0 0 SAM 1 1 0 1 0 0 SARAH 1 1 0 0 1 0 TIM 1 1 0 0 0 1 TINA 1 0 1 1 0 0 VERNA 1 0 1 0 1 0 VIC 0 1 0 1 0 1;
Example: Solution procedure
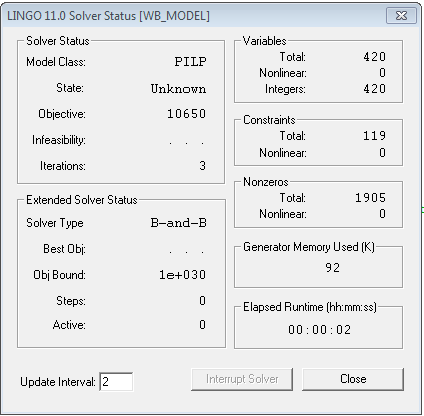
- What is a better objective value upper bound?
- 15 cars that cost $10 per day
- 6 days each car can be rented
- $900
Example: Solution procedure
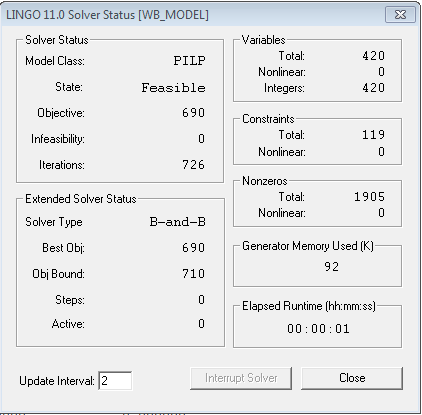
- A feasible integer solution has been found
- A tighter bound has been achieved
Example: Solution procedure
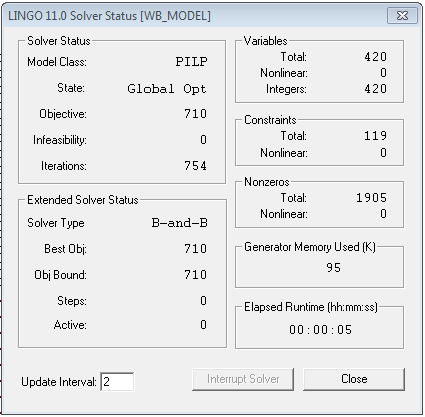
- An integer solution that matches the objective upper bound has been found
- This solution is optimal
Thanks
LINGO Model
SETS: CAR: COST; CUSTOMER: M, T, W, R, F, S; DV (CAR, CUSTOMER): X; ENDSETS DATA: CAR COST= CAR1 10 CAR2 10 CAR3 10; CUSTOMER M T W R F S= ABBY 1 1 0 0 0 0 AL 0 0 1 1 1 1 BARB 1 1 1 1 1 0 BRUCE 0 1 1 1 0 0 CARL 1 1 1 0 0 0 CINDY 0 0 0 1 1 1; ENDDATA
LINGO Model
MAX = @SUM(CAR( I):
@SUM(CUSTOMER( J):
!Days customer J needs a car;
(M( J) + T( J) + W( J) + R( J) + F( J) + S( J))*
!Cost of renting car I per day;
COST( I) *
!Decision to rent car J to cutomer I;
X( I, J)));
!Each customer gets at most one car;
@FOR(CUSTOMER( J):
@SUM(CAR( I): X( I,J)) <= 1);
!Each car has at most one customer on Monday;
@FOR(CAR( I):
@SUM(CUSTOMER( J): M( J)*X( I, J)) <= 1);
!Each car has at most one customer on Tuesday;
@FOR(CAR( I):
@SUM(CUSTOMER( J): T( J)*X( I, J)) <= 1);
LINGO Model
!Each car has at most one customer on Wednesday; @FOR(CAR( I): @SUM(CUSTOMER( J): W( J)*X( I, J)) <= 1); !Each car has at most one customer on Thursday; @FOR(CAR( I): @SUM(CUSTOMER( J): R( J)*X( I, J)) <= 1); !Each car has at most one customer on Friday; @FOR(CAR( I): @SUM(CUSTOMER( J): F( J)*X( I, J)) <= 1); !Each car has at most one customer on Saturday; @FOR(CAR( I): @SUM(CUSTOMER( J): S( J)*X( I, J)) <= 1); !Binary variable for each car customer combination @FOR(CAR( I): @FOR(CUSTOMER( J): @BIN(X( I,J))));
