Integer programming for instance selection in supervised learning
Walter Bennette
02-28-2014
Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
What is classification?
How Companies Learn Your Secrets
Target used data mining to determine when customers became pregnant.
What is classification?
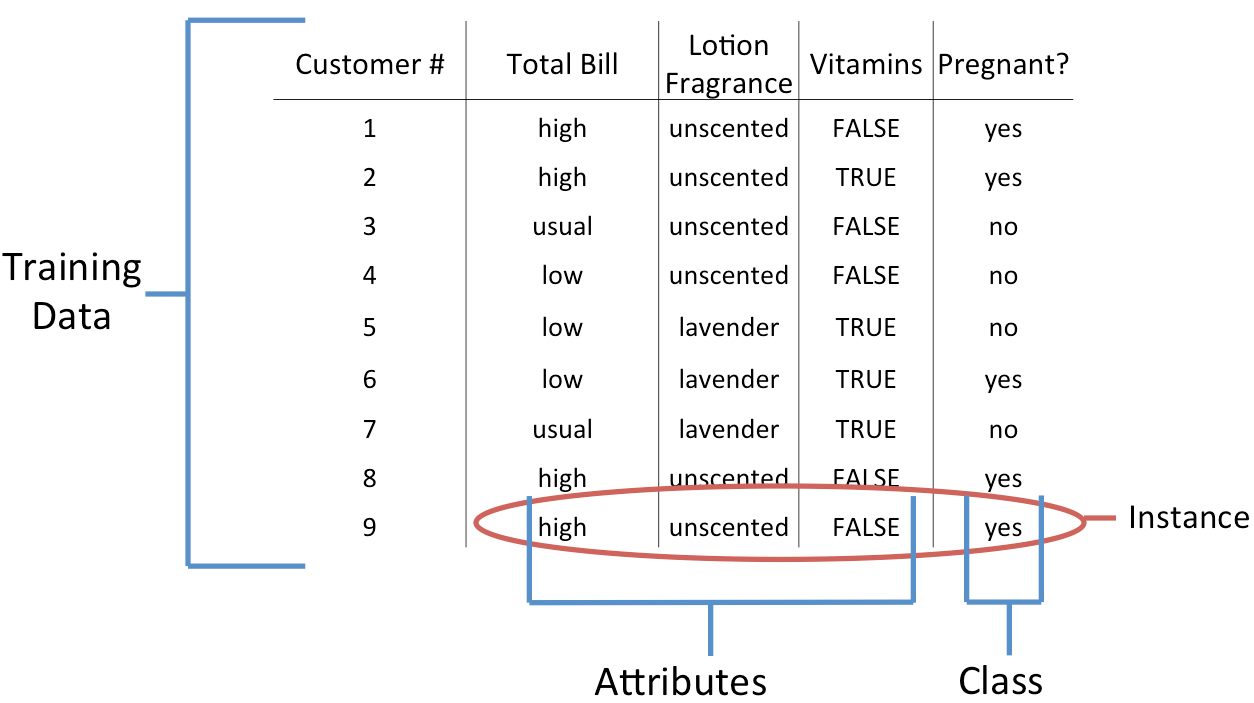
What is classification?
A classifier is a scheme built from training data to classify unlabeled data.
The decision tree classifier builds a model that tries to split the data into homogeneous groups.
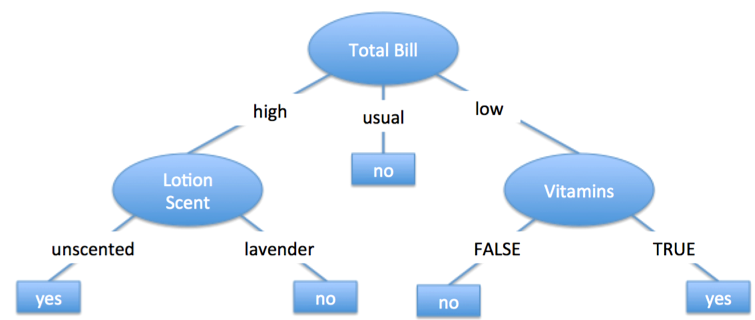
What is classification?
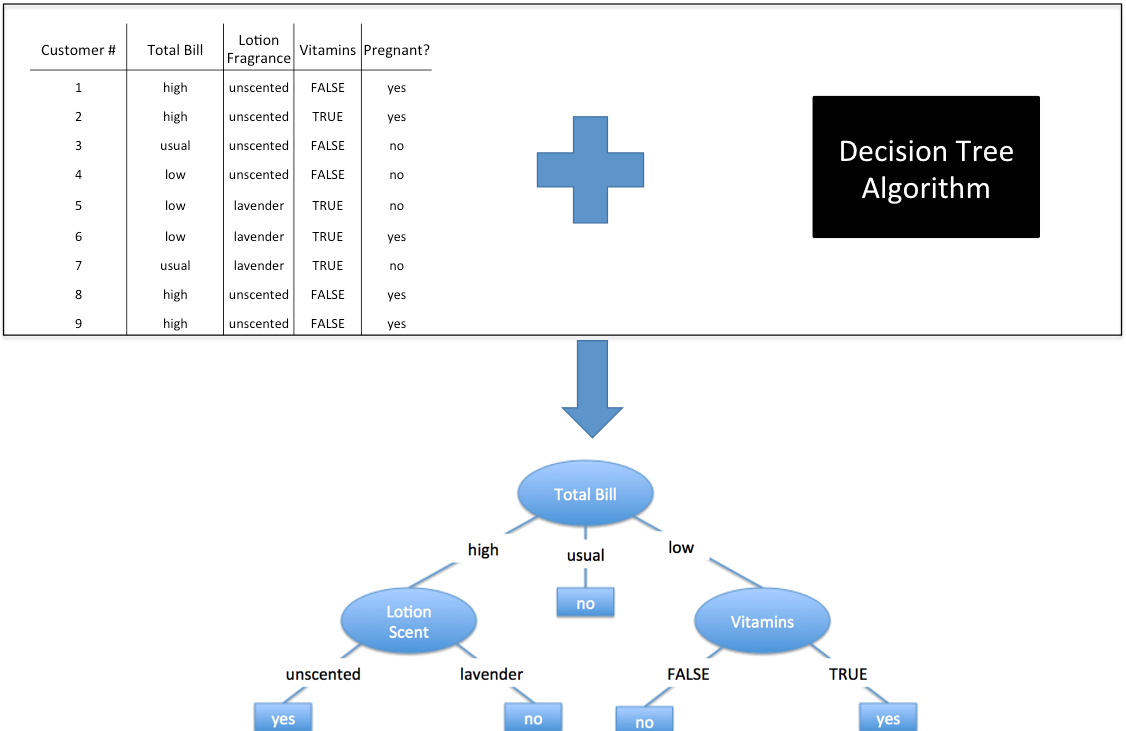
What is classification?
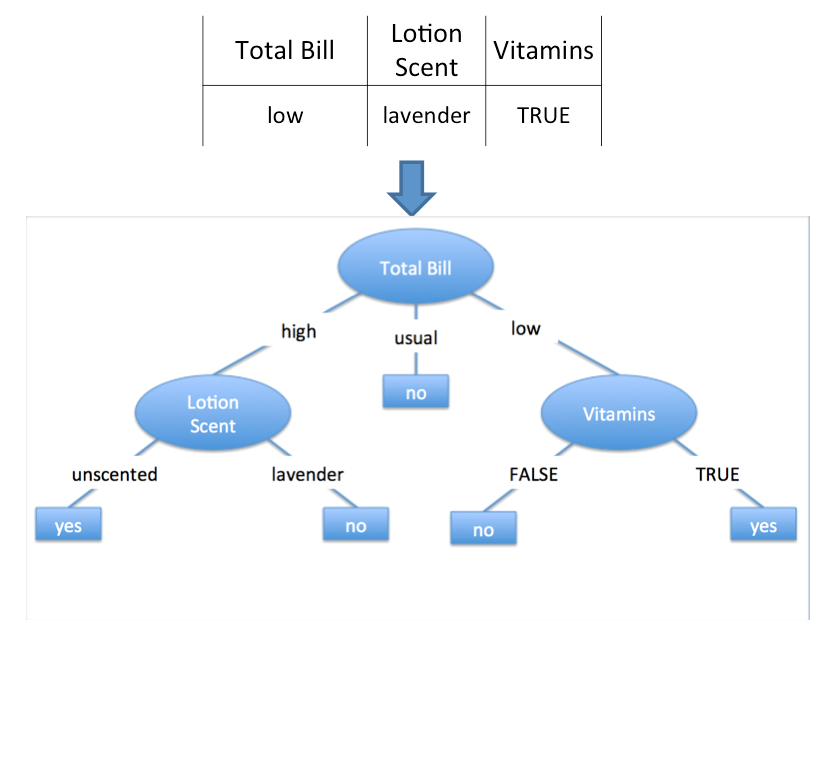
What is classification?
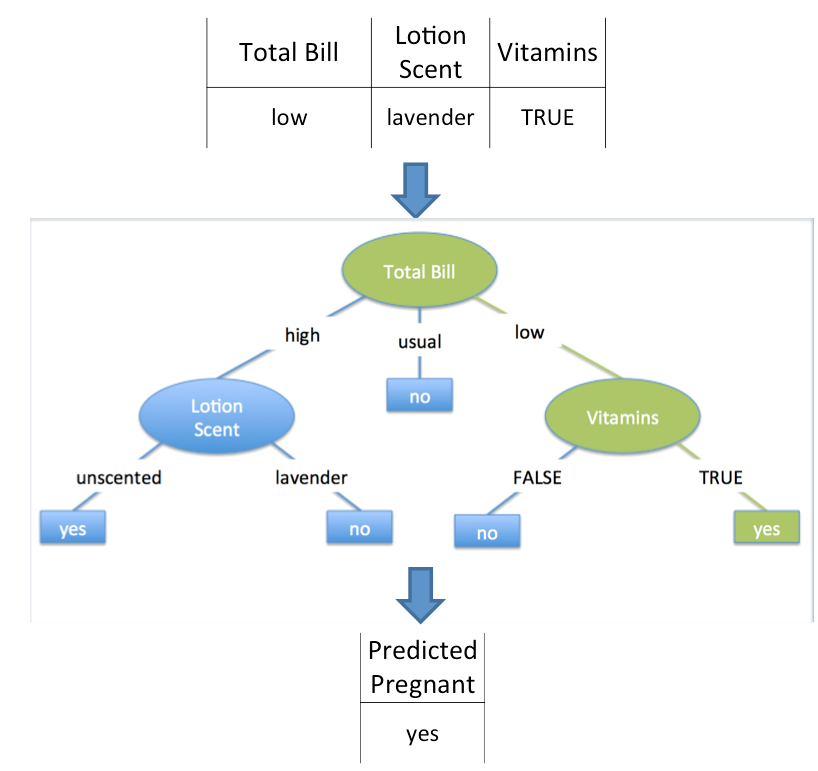
What is classification?
Test accuracy is found by making predictions on previously unseen data.
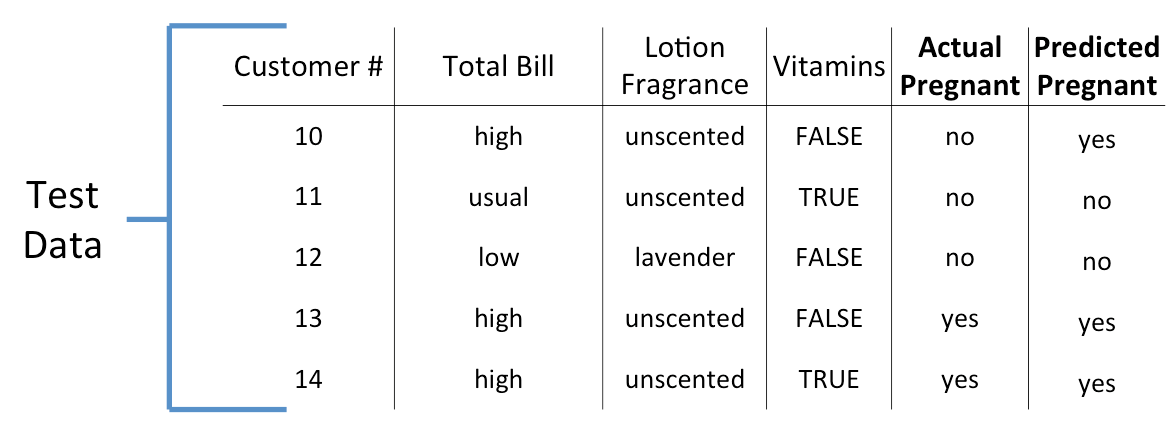
We say the decision tree has 80% test accuracy because four of the five predictions are correct.
Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Why do we want better classifiers?
Classification models can be useful in a variety of application areas
- Retail
- Healthcare
- Finance
Better (or classifiers with higher testing accuracy) are beneficial
- Make fewer missclassifications
- Gain useful knowledge when analyzing the classifier
Questions????

Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Motivation
Aspects of training data may make it difficult to build/induce/learn an accurate classifier
We believe that selecting which instances to learn from can improve the accuracy of a classifier. This is called instance selection!
Motivation
Classes may overlap
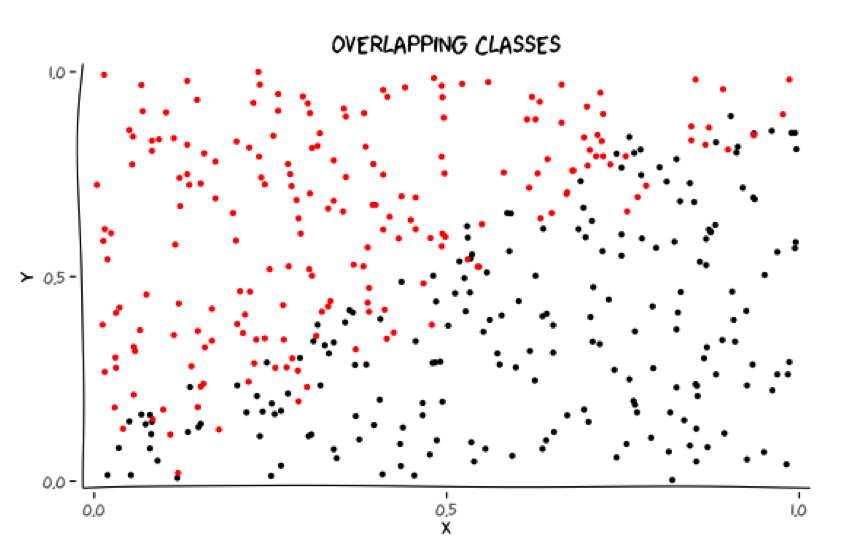
Where should these classes be separated?
Motivation
Classes may overlap
Where should these classes be separated?
Motivation
Classes may overlap
Where should these classes be separated?
Motivation
Classes may overlap
Where should these classes be separated?
Motivation
Classes may have outliers
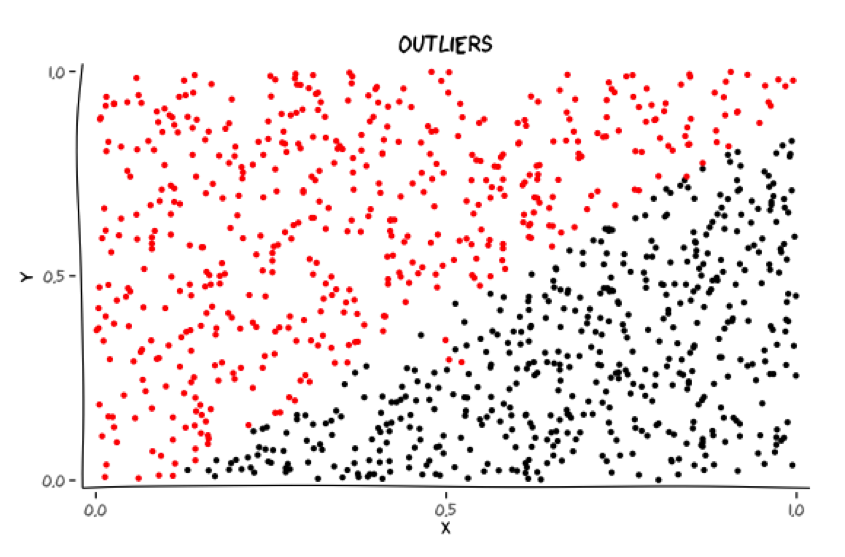
Should these outliers be accommodated?
Motivation
Classes may have outliers
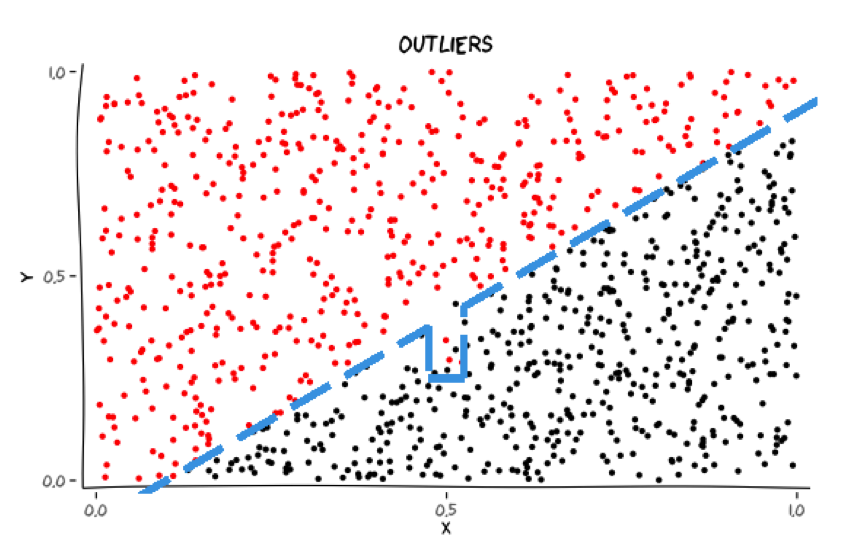
Should these outliers be accommodated?
Motivation
Minority class
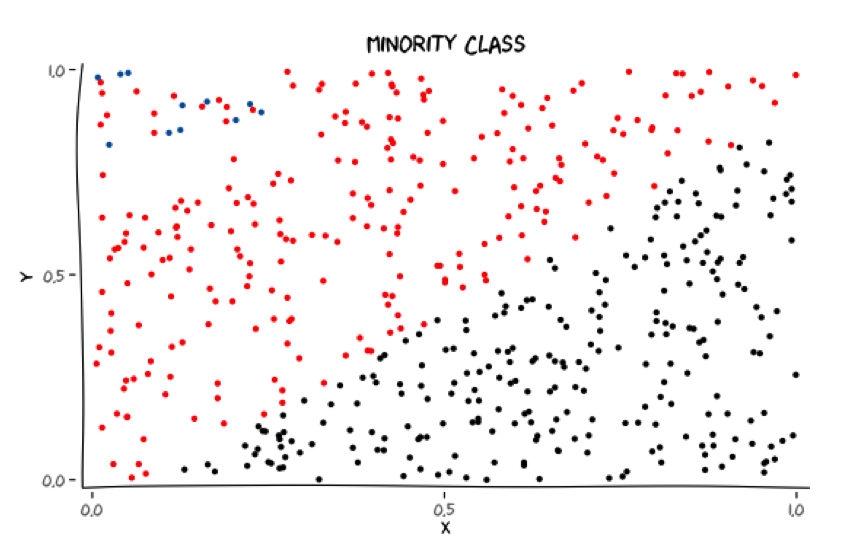
Does capturing the minority class introduce unnecessary structure?
Motivation
Minority class
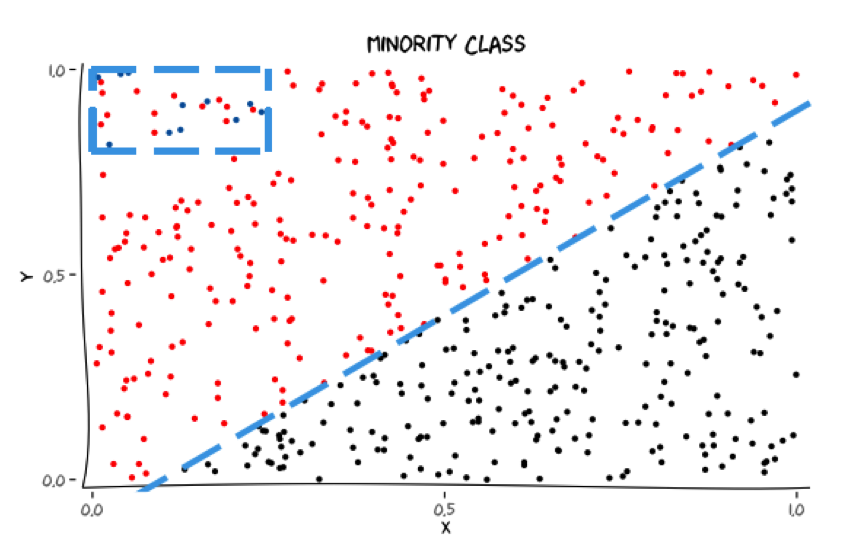
Does capturing the minority class introduce unnecessary structure?
Motivation
Instance selection can address issues in the training data by creating a subset of the original data
The intention is that the classification algorithm will perform better when learning from the selected/reduced data set
Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Explanation
Explanation
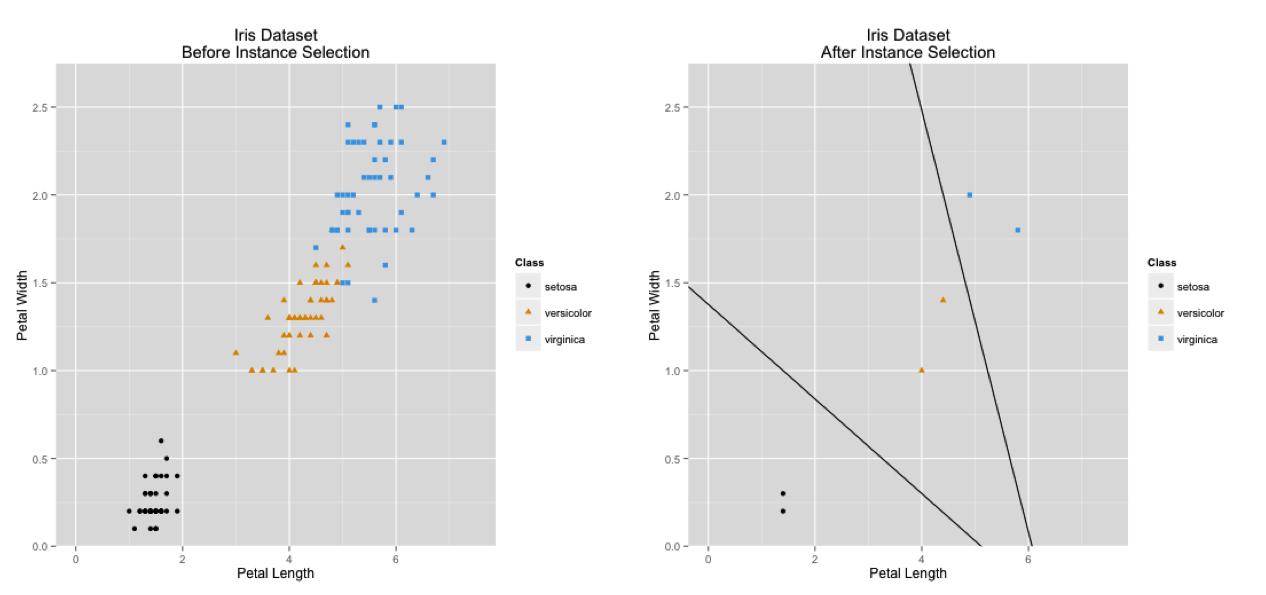
Explanation
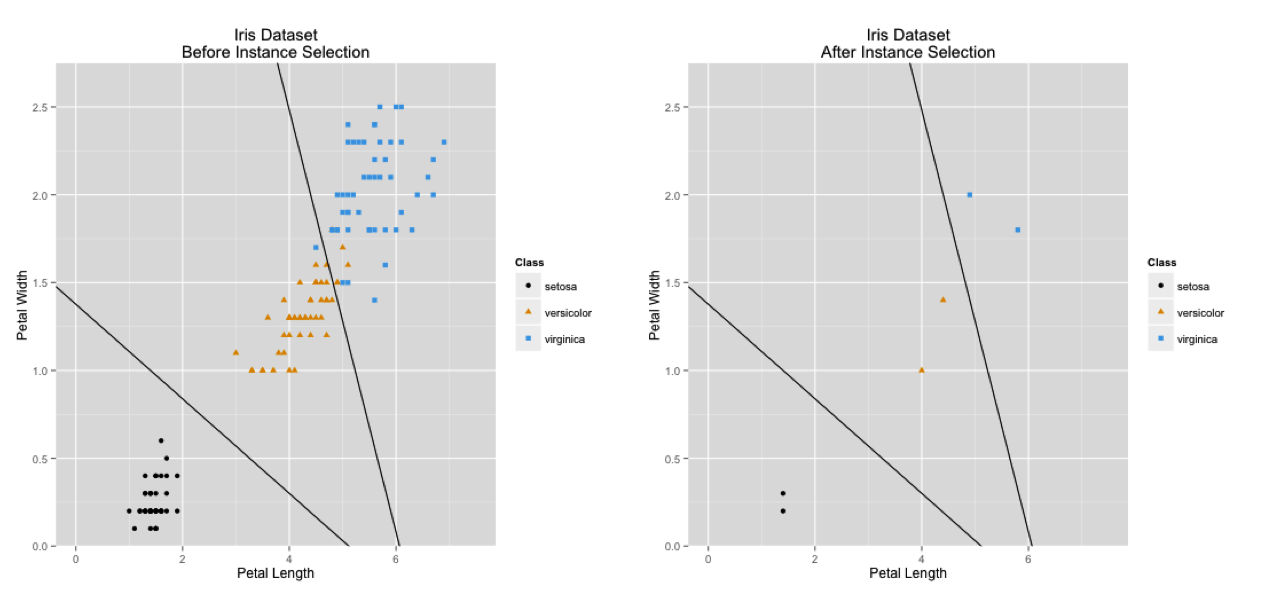
Explanation
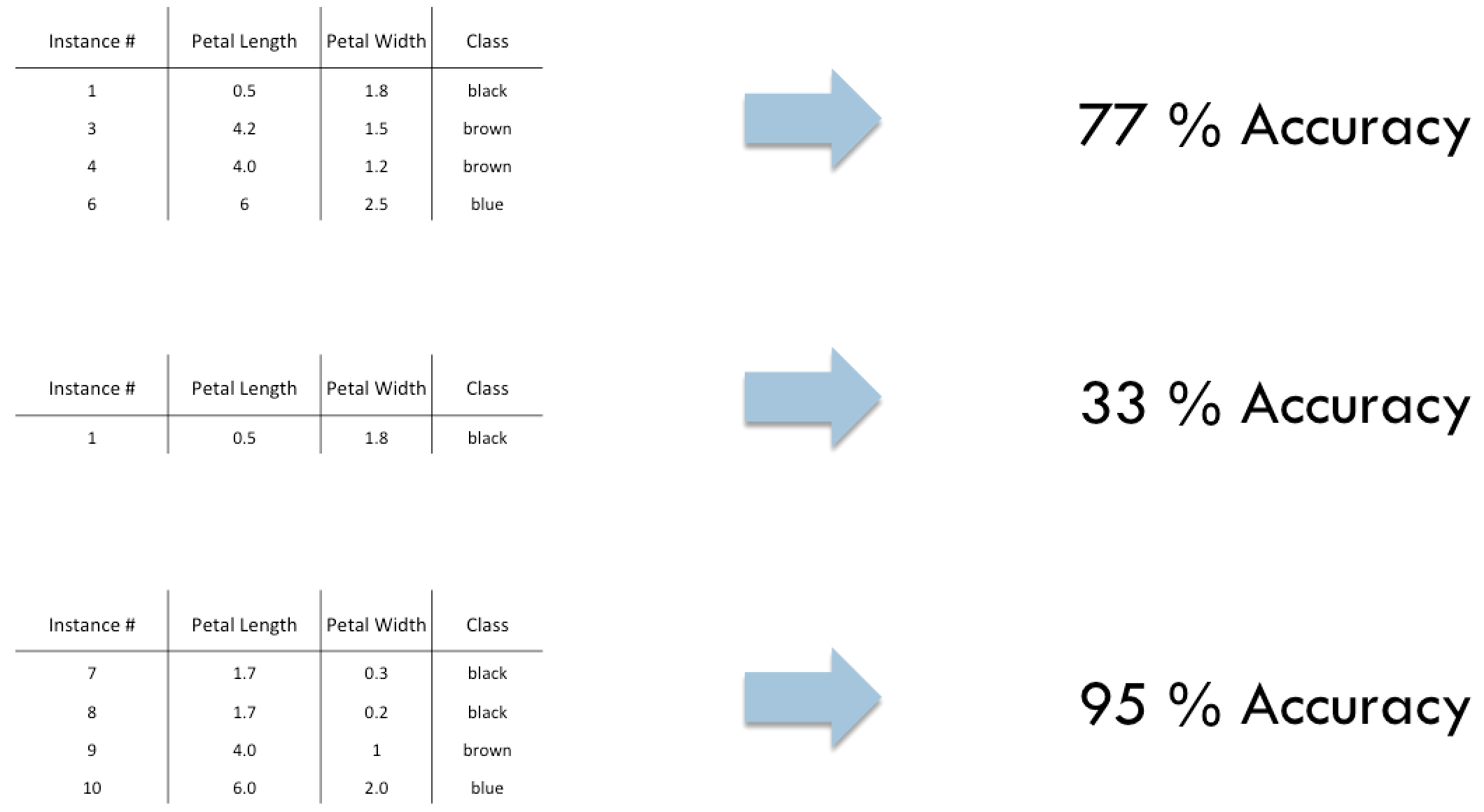
Explanation
Instance selection is a combinatorial optimization problem
- Each instance is included or not included in the selected training data
Goal: maximize classifier accuracy
- No closed form objective function
- \( 2^n \) subsets for a dataset of size \( n \)
Good?

Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Past formulation
\( {\mathbf {Max} \ \ \ \ Classifier \ Accuracy \\ \mathbf {s.t} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ x_i \in \{0,1\} \ \forall \ i \in I} \)
- \( I \ \) is the set of all instances
- The decision is whether or not to include an instance in the new training data
Past formulations
A VAST majority rely on evolutionary algorithms to solve this problem.
Other combinatorial optimization problems look similar to instance selection if the problem is reformulated. This allows us to take advantage of optimization theory.
How it feels to find the gap in literature

Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
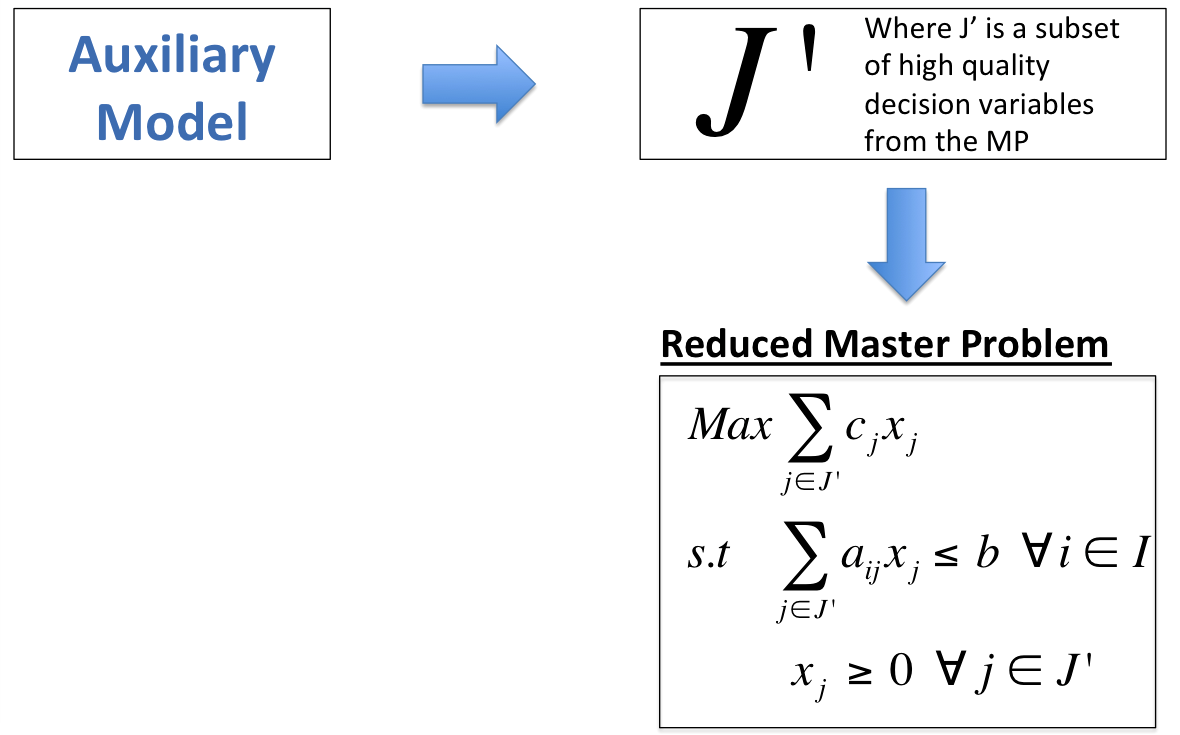
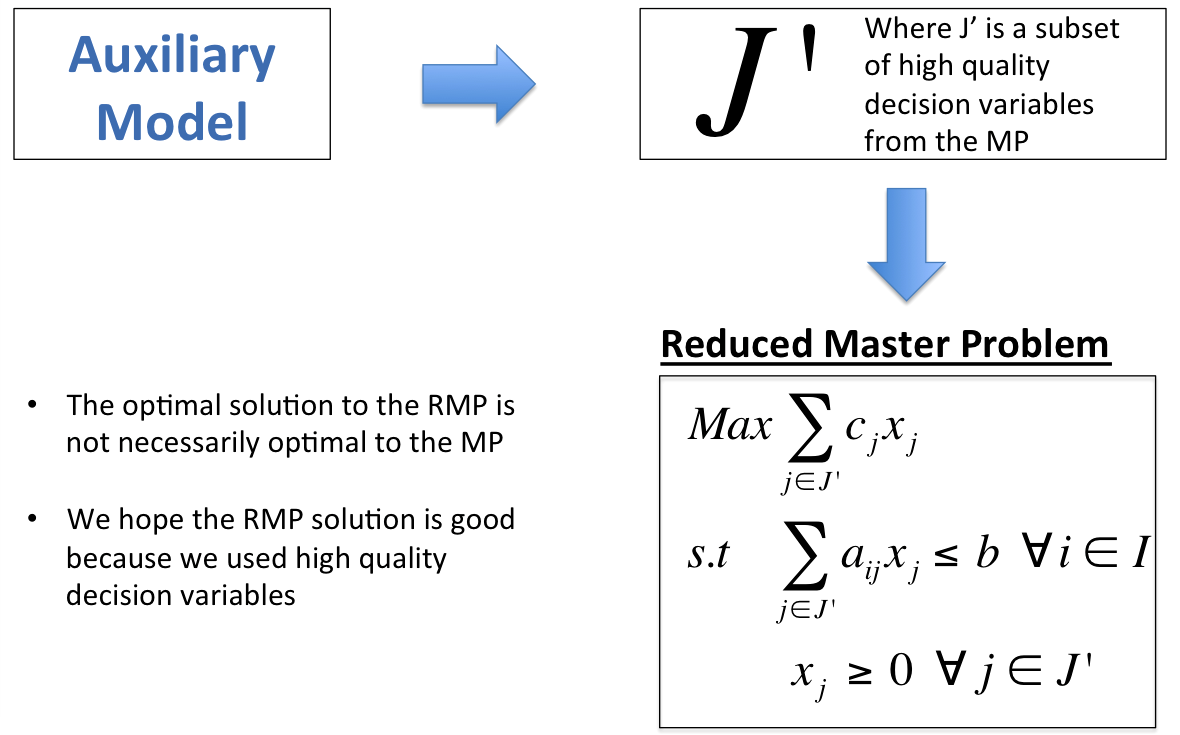
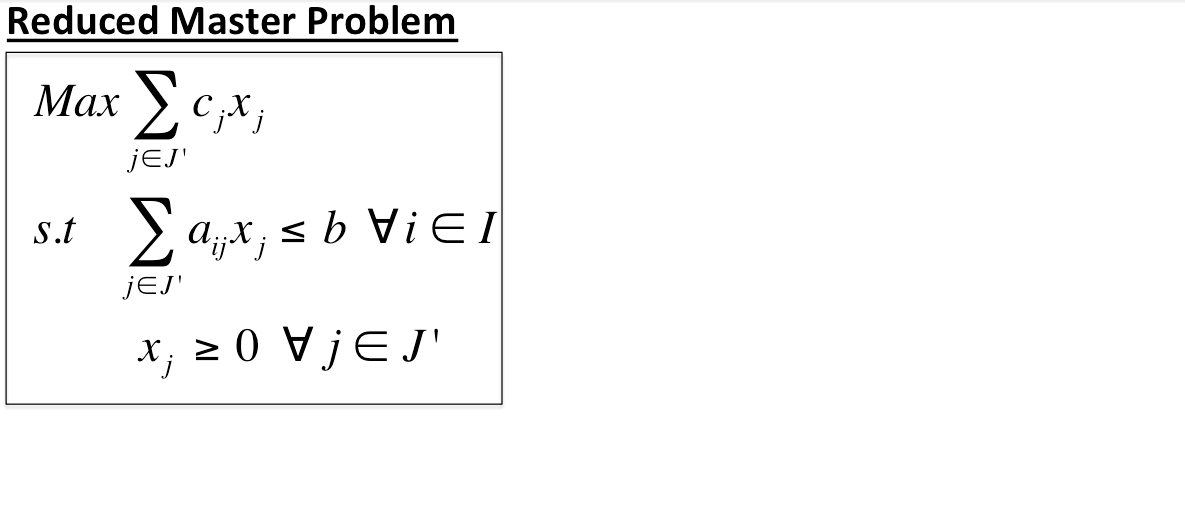
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
<—A column is
associated with each
possible subset of
instances
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
<— Select at most one
column
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
<— \( a_{ij} \) indicates if instance
\( i \ \) is in column \( \ j \)
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
<— \( c_j \) is the accuracy of a
classifier built from
the contents in column
\( \ j \)
Instance selection reformulation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
<—For a dataset of size \( n \)
there are \( 2^n \) decision
variables
Enter COLUMN GENERATION!!
Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Results
Column generation
A technique to solve linear programs with a huge number of decision variables
- Too many variables to solve quickly
- Too many variables to even enumerate them all
Commonly extended to integer programs
- Relax integrality constraints
- Branch and price
Column generation

Column generation

Column generation: Type I

Column generation: Type I
Column generation: Type I
Column generation: Type I
Column generation: Type II
Exploit a feature of the simplex algorithm to guarantee that the optimal solution of the master problem is found
Let us have a quick reminder of how simplex works
Column generation: Type II
- Given a feasible solution to \( \left \{max \ c^Tx: Ax \le b, x \ge 0 \right \} \)
- The solution can be written as the variables belonging to the basis and the variables belonging to the non-basis
- Simplex works toward the optimal solution of the LP by switching a variable in the non-basis for one in the basis
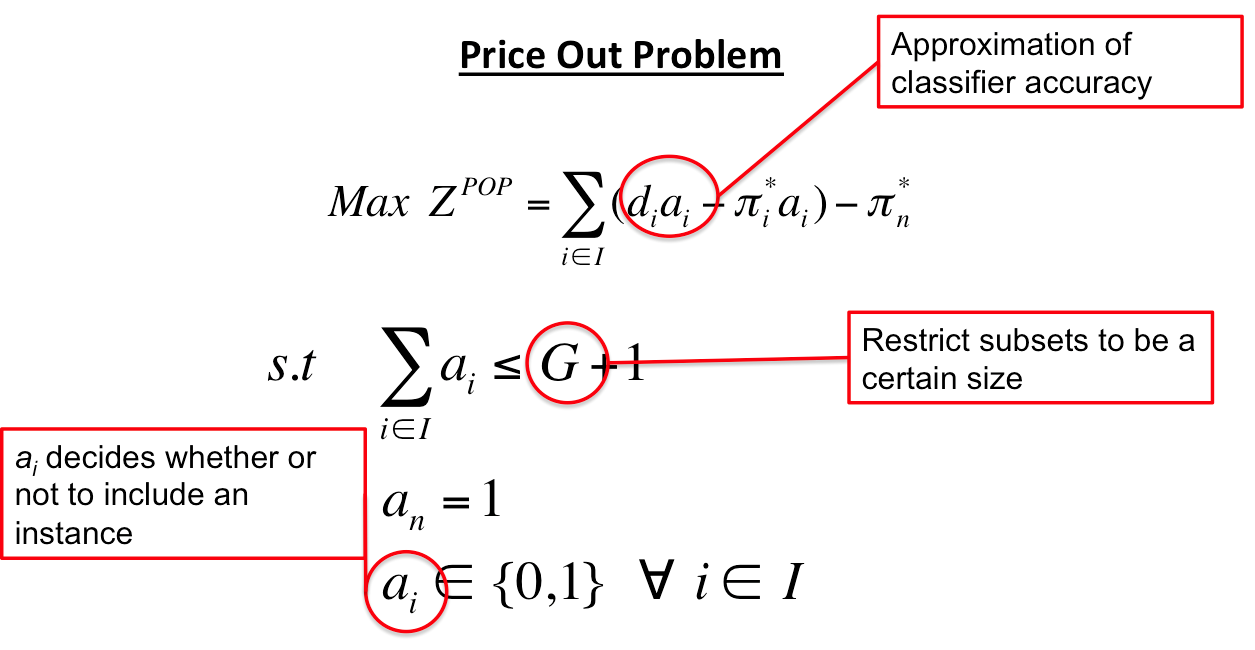
- For a non-basis variable \( j \), \( \ Reduced \ Cost_j = \left \{c_j-\pi^Ta_j \right \} \)
- \( c_j \ \) is the objective coefficient of variable \( j \)
- benefit from including variable \( j \) in basis
- benefit from including variable \( j \) in basis
- \( a_j \ \) is the column of the A matrix associated with variable \( j \)
- \( \pi \ \) is the simplex multiplier of the LP
- cost of including variable \( j \ \) in basis
- \( c_j \ \) is the objective coefficient of variable \( j \)
Column generation: Type II
Column generation: Type II
Column generation: Type II
Column generation: Type II
Column generation: Type II
Column generation: Type II
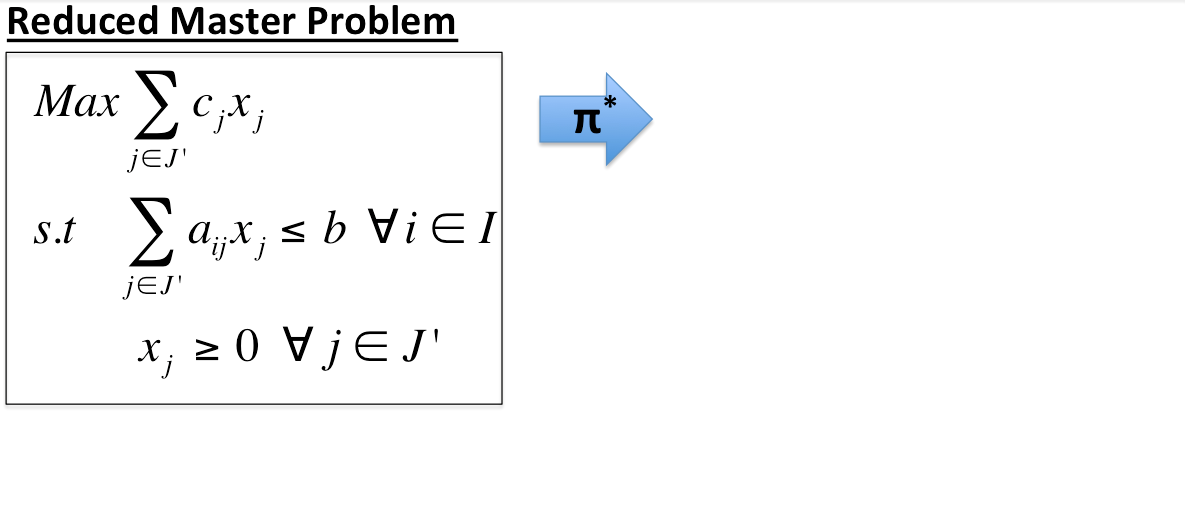
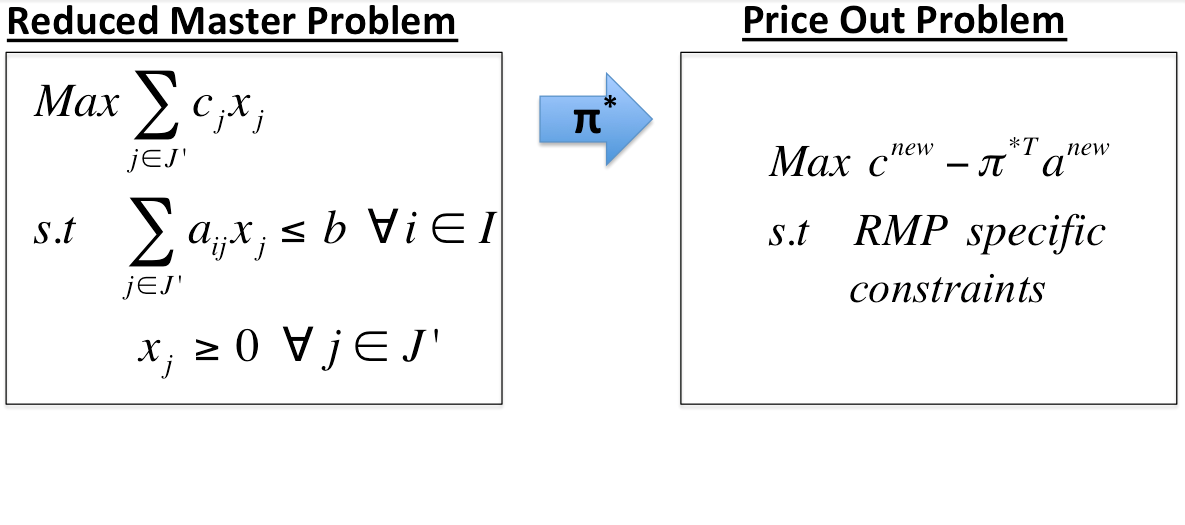
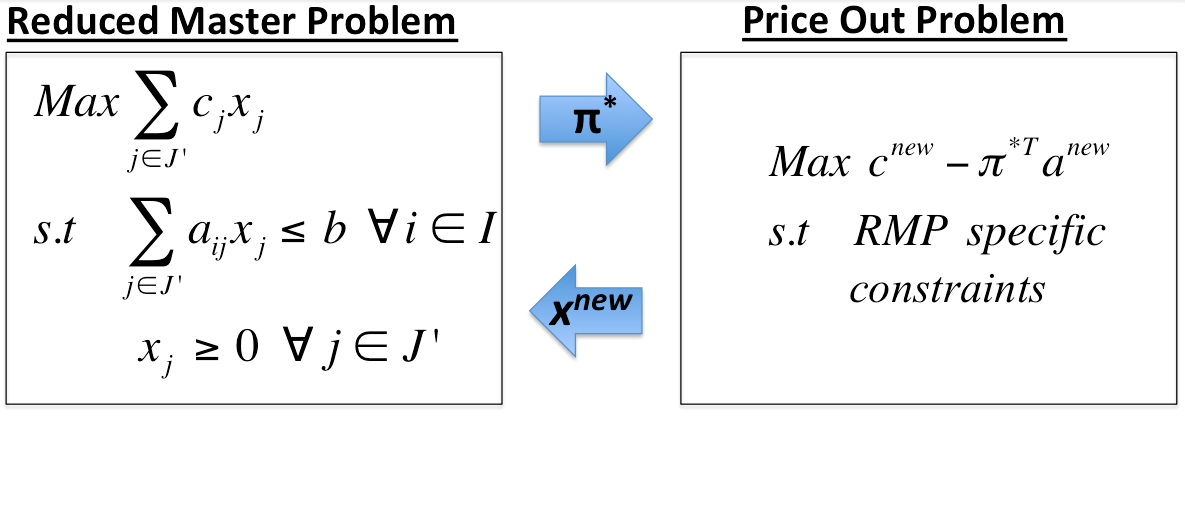
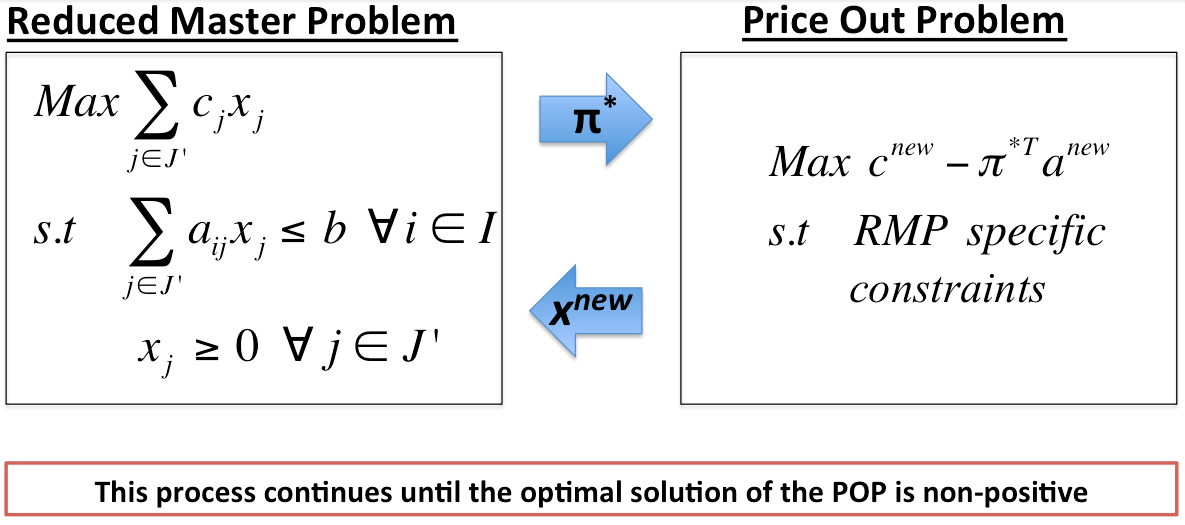
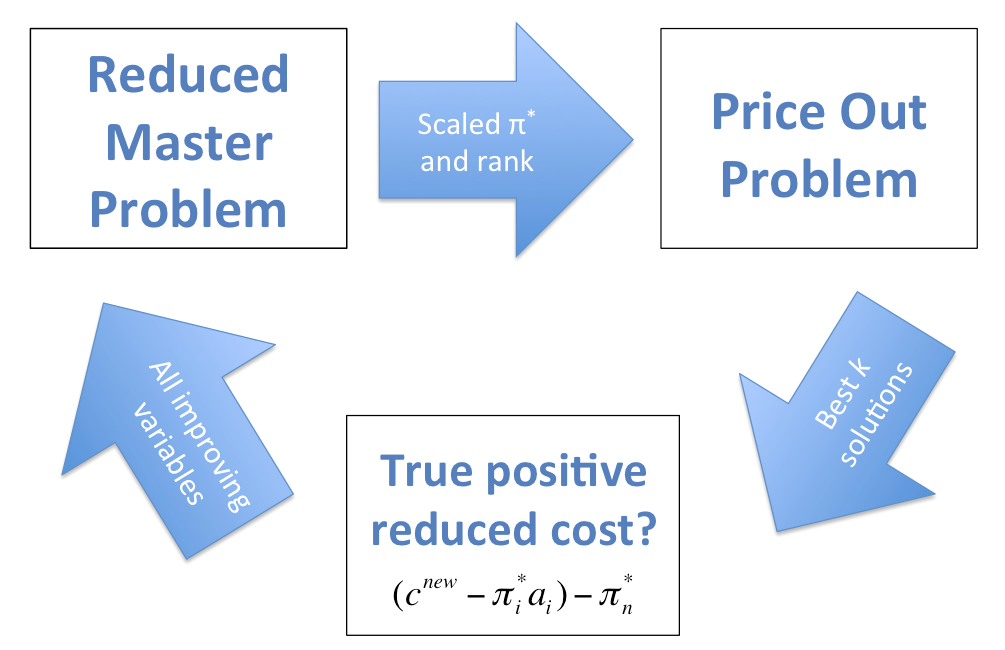
Process
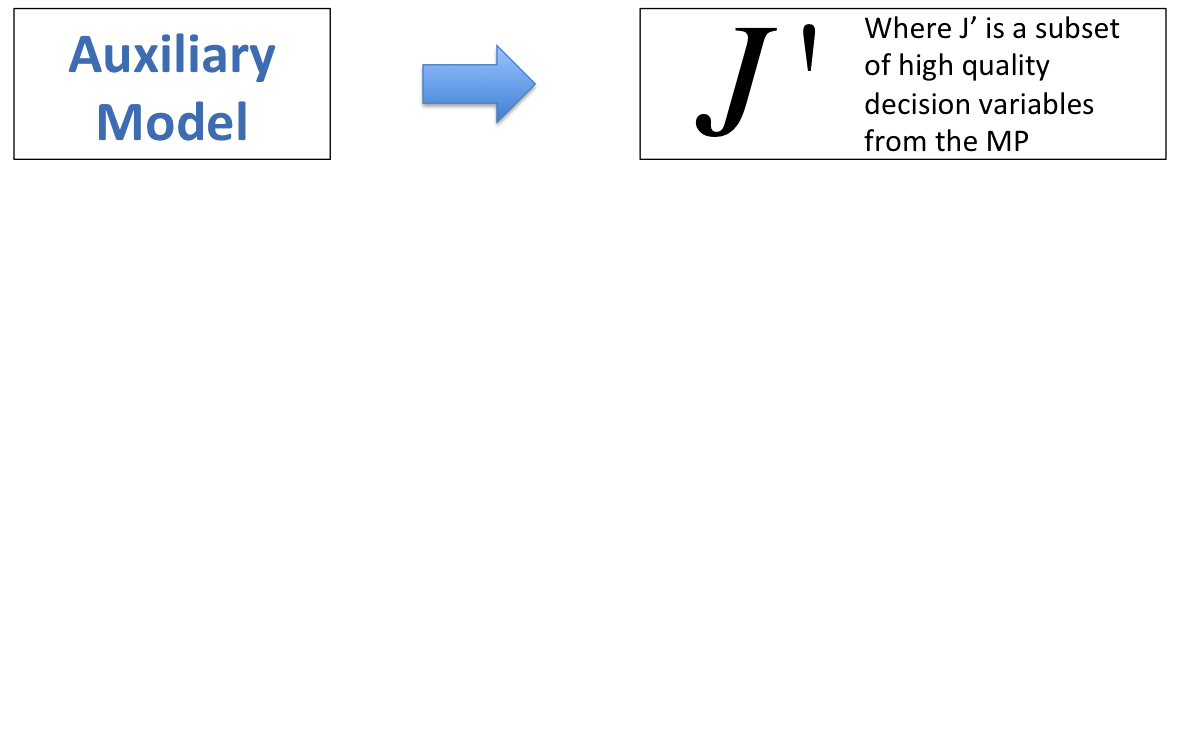
- Generate a subset of variables, \( J' \), from the MP
- Use \( J' \) to define the RMP
- Solve the RMP for optimal dual variables \( \pi^* \)
- Solve the POP
- If the optimal solution is positive add \( x^{new} \) to \( J' \)
- If the optimal solution is non-positive then the optimal solution to the RMP is optimal to the MP
How's everyone doing?

Implementing Column Generation
\( \mathbf {Max} \ \ \ \sum_{j \in J}c_jx_j \)
\( \mathbf {s.t} \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}a_{ij}x_j \le 1 \ \ \forall \ i \in I \)
\( \ \ \ \ \ \ \ \ \ \ \sum_{j \in J}x_j \le 1 \)
\( \ \ \ \ \ \ \ \ \ \ \ x_j \in \{0,1\} \ \ \forall \ j \in J \)
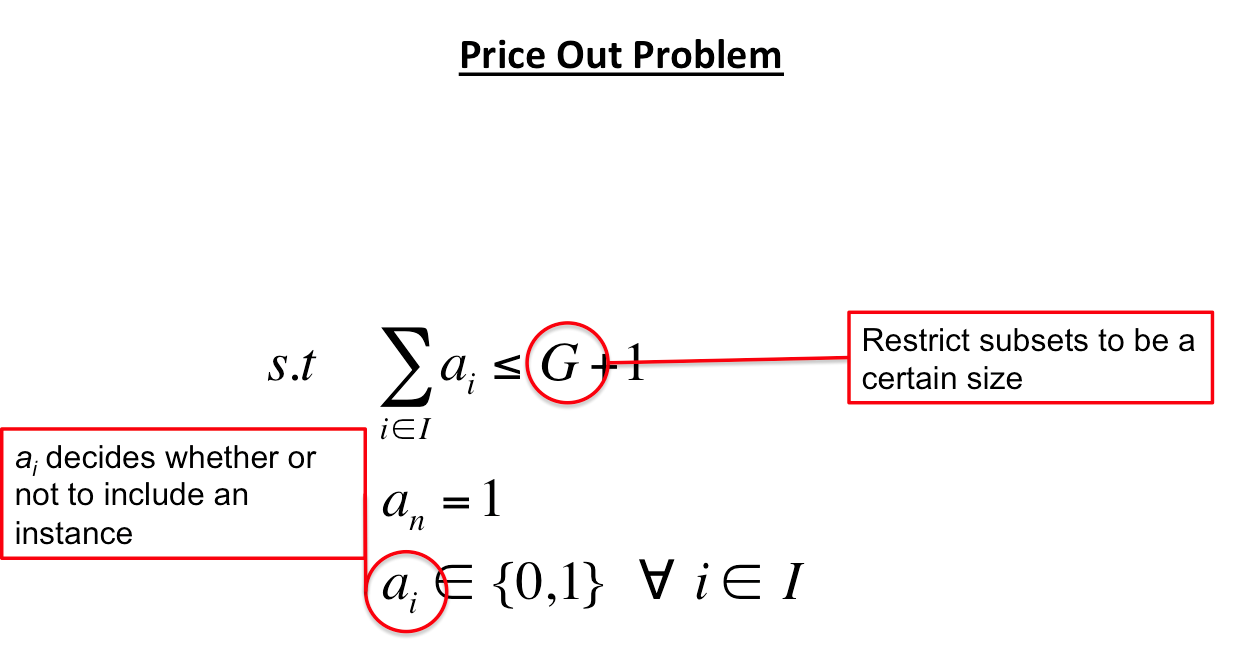
<—For a dataset of size \( n \)
there are \( 2^n \) decision
variables
Implementing Column Generation

Implementing Column Generation

Implementing Column Generation

Implementing Column Generation
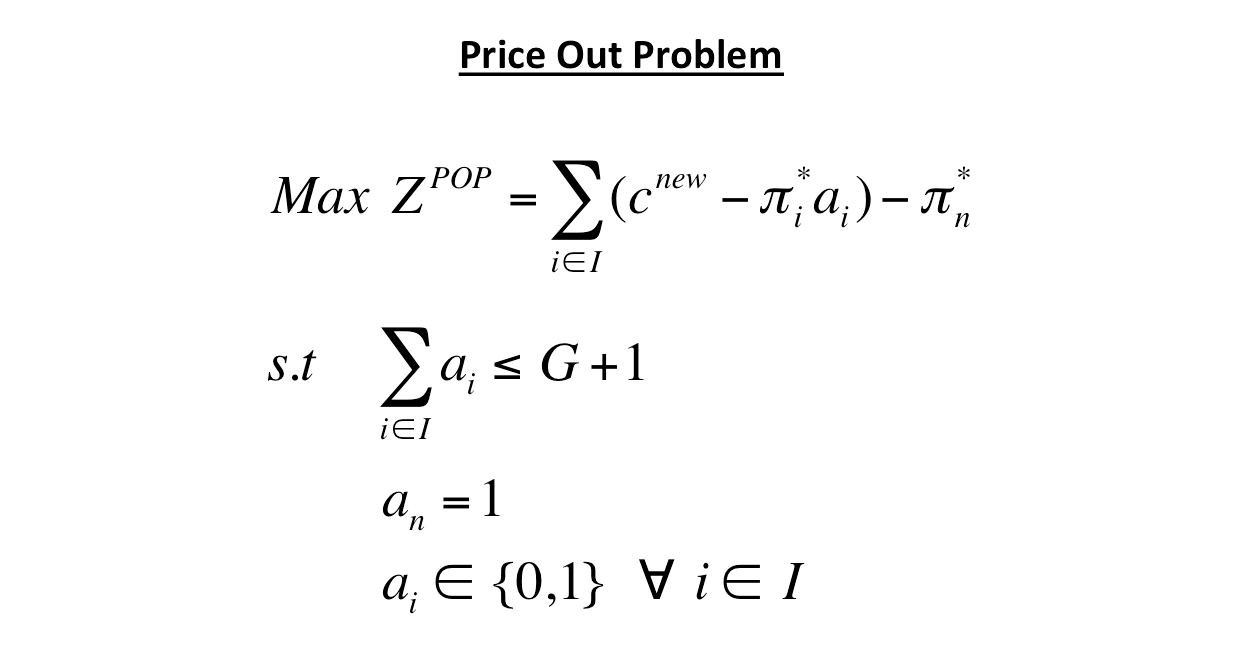
Implementing Column Generation
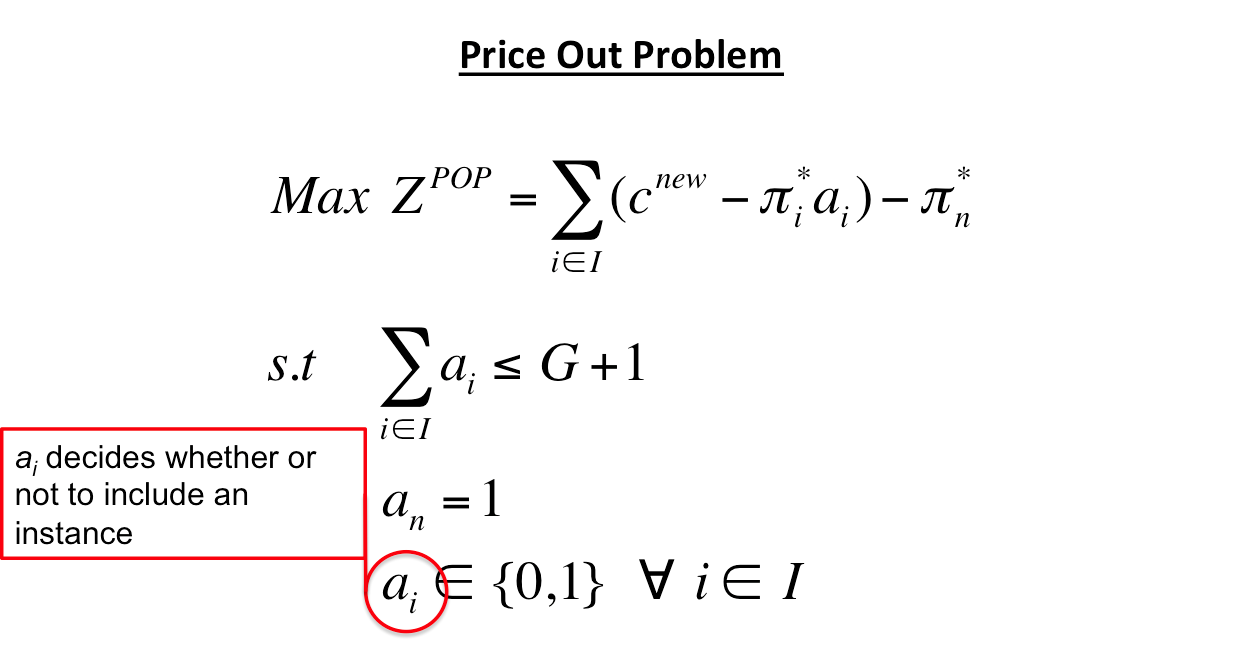
Implementing Column Generation

Implementing Column Generation

Implementing Column Generation
Implementing Column Generation

Implementing Column Generation
Implementing Column Generation
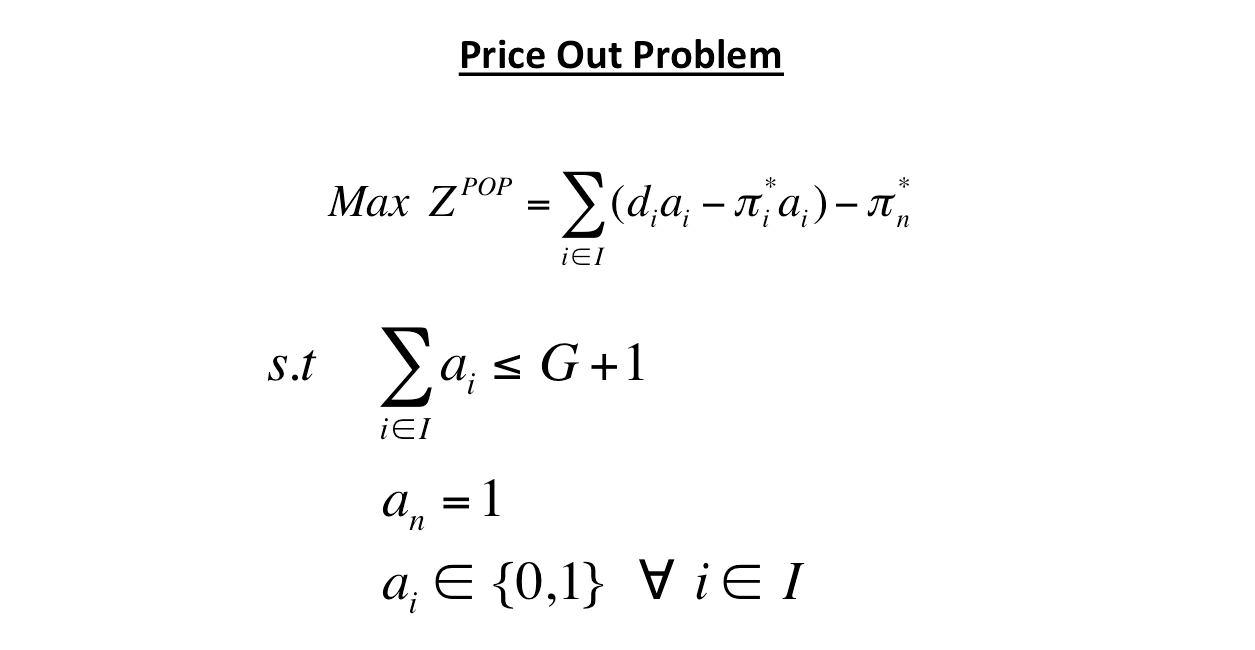
Implementing Column Generation
Whew! Technical details are done.

Outline
- Classification
- What is classification?
- Why do we want better classifiers?
- Instance selection
- Motivation
- Explanation
- Past formulation
- Instance selection reformulation
- Reformulation
- Column generation
- Reformulation
- Interesting Results
Interesting Results
Statlog (Landsat Satellite) dataset
- Classify pixels of an image
- 37 attributes
- 296 instances
- 6 classes
- UCI machine learning repository
Interesting Results
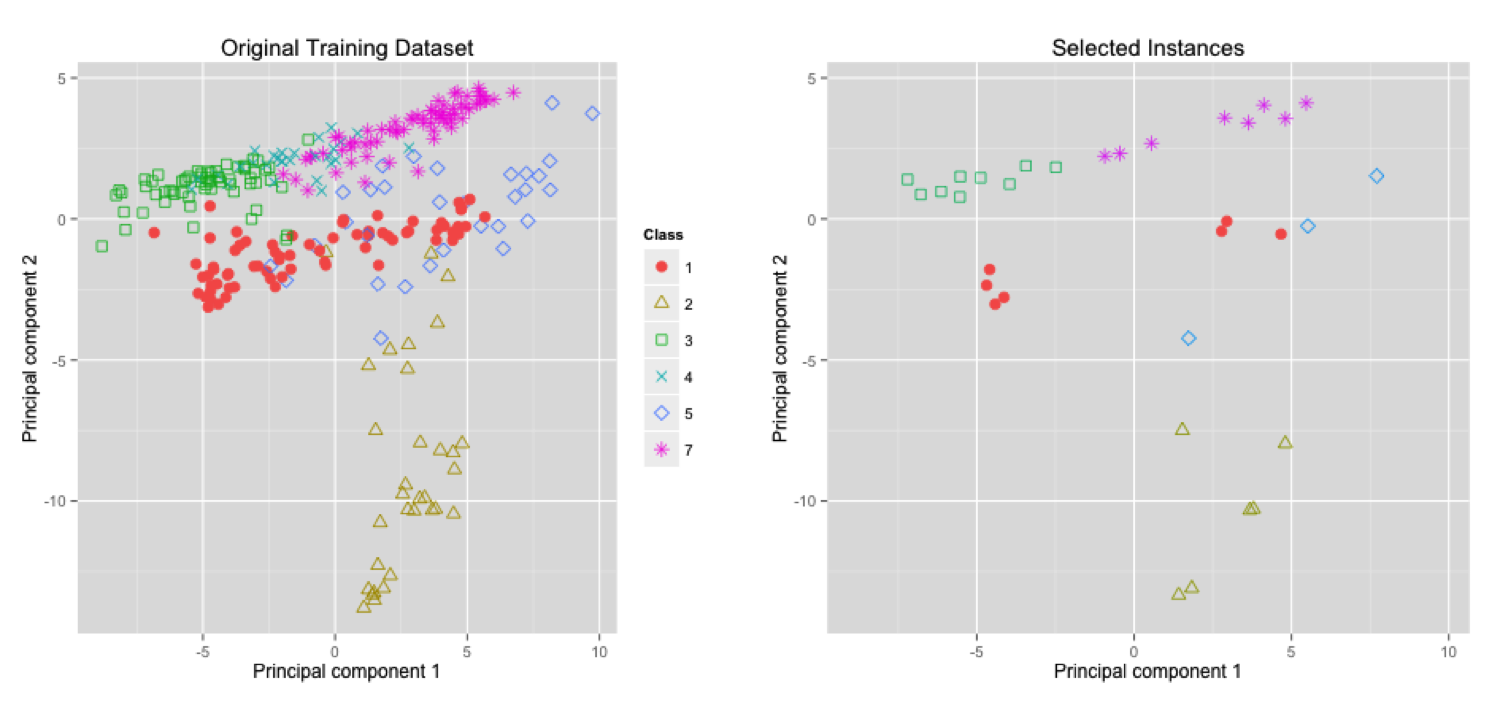
Interesting Results
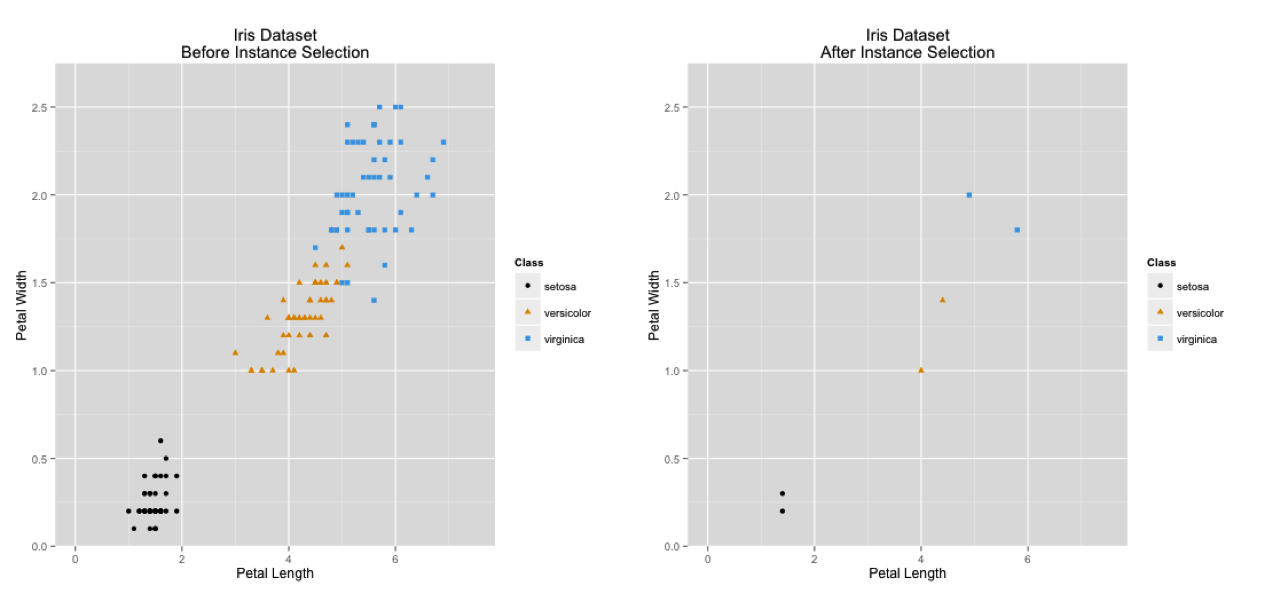
Showing the effect of instance selection on a naive Bayes classifier. Average test accuracy is reported.
| Dataset | Original | Instance Selection |
|---|---|---|
| Balance | 90% | 91% |
| Chess | 84% | 90% |
| Credit Approval | 78% | 85% |
| E-coli | 83% | 83% |
| Statlog | 80% | 83% |
| Tic-Tac-Toe Endgame | 70% | 72% |
Conclusion
Integer programming techniques can help us solve the instance selection problem
Instance selection manipulates the training data to allow classifiers to take greater advantage of the data
- overlapping classes
- outliers
- minority classes